Determinación del Coheficiente Hall
Para un campo Magnético Constante
Debemos reparar en que la linea que une los puntos en los que
medimos la diferencia de potencial no es perfectamente perpendicular a la
dirección de la intensidad que circula por la muestra (ver figura 4). Eso
va a causar que la diferencia de potencial que medimos no sea debida
enteramente al efecto Hall.
Antes
de nada se calculara la corrección que debemos emplear debido a este fenómeno.
Para ello, hagamos mediciones del efecto Hall sobre la
muestra, pero con campo magnético
B = 0. Contrariamente a lo que cabría esperar viendo la expresión
(1), la diferencia de potencial medida con el voltímetro no es 0.
Para corregir este problema, representaremos los datos así
obtenidos y restaremos la expresión de la recta resultante de la regresión
a la de la recta que conseguimos sin tener en cuenta este fenómeno.
Los datos medidos cuando B=0 son:
|
I (mA) |
ERROR DE I |
V (mV) |
ERROR DE V |
|
|
0.0 |
0.1 |
0.0 |
0.1 |
|
|
11.0 |
0.1 |
-9.4 |
0.1 |
|
|
20.5 |
0.1 |
-17.4 |
0.1 |
|
|
30.8 |
0.1 |
-26.2 |
0.1 |
|
|
40.9 |
0.1 |
-34.8 |
0.1 |
|
|
59.3 |
0.1 |
-50.5 |
0.1 |
|
Cuya gráfica es:
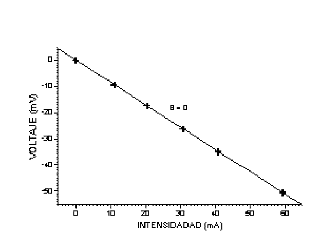
fig. 6 |
El resultado de la regresión:
|
Linear Regression for DATA1_B: Y = A + B * X Param
Value sd A
0.00625
0.02415 B
-0.85131
0.00072 R = -1 SD = 0.03455, N = 6 P = 3.1374E-12 |
|
Ahora procedamos al análisis de datos obtenidos para un
campo B constante y distinto de 0.
Fijaremos la intensidad que circula por las espiras a un
valor determinado (1.99 A en nuestro caso), con lo que
también fijaremos el campo magnético al que someteremos
la muestra.
A continuación iremos variando la intensidad I que circula
por la muestra y, para cada uno de estos valores,
mediremos con el voltímetro el voltaje Hall UH
(ver figura 4).
Obtenemos así los siguientes datos:
|
I (mA) |
ERROR DE I |
V (mV) |
ERROR DE V |
|
|
-52.4 |
0.1 |
115.7 |
0.1 |
|
|
-44.8 |
0.1 |
99.2 |
0.1 |
|
|
-37.8 |
0.1 |
84.0 |
0.1 |
|
|
-34.0 |
0.1 |
35.3 |
0.1 |
|
|
-28.9 |
0.1 |
63.9 |
0.1 |
|
|
-18.6 |
0.1 |
41.0 |
0.1 |
|
|
-12.3 |
0.1 |
27.1 |
0.1 |
|
|
-8.5 |
0.1 |
18.4 |
0.1 |
|
|
0 |
0.1 |
0.0 |
0.1 |
|
|
11.2 |
0.1 |
-25.2 |
0.1 |
|
|
15.3 |
0.1 |
-34.4 |
0.1 |
|
|
20.1 |
0.1 |
-45.2 |
0.1 |
|
|
26.6 |
0.1 |
-59.7 |
0.1 |
|
|
30.4 |
0.1 |
-68.4 |
0.1 |
|
|
38.9 |
0.1 |
-87.2 |
0.1 |
|
|
42.6 |
0.1 |
-96.0 |
0.1 |
|
|
51.7 |
0.1 |
-116.4 |
0.1 |
|
|
60.1 |
0.1 |
-135.2 |
0.1 |
|
Representemos el voltaje Hall frente a la intensidad y
mediante una regresión
lineal calculemos su
pendiente:
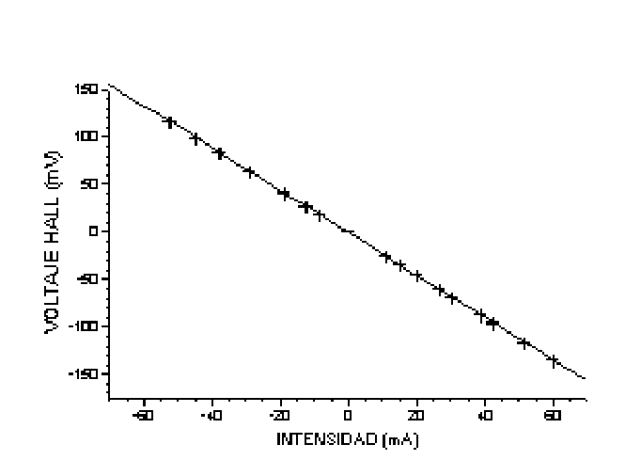
fig. 7 |
La regresión lineal de estos datos da como resultado:
|
Linear Regression for DATA1_B: Y = A + B * X Param
Value
sd A
-0.55691
0.0868 B
-2.23218
0.00256 R = -0.99999 SD = 0.35313, N = 17 P = 1.0262E-36 |
|
De donde concluimos que la pendiente de la curva es
-2.232+/-0.003.
Teniendo en cuenta la fuente de error comentada al principio
de esta sección y
el calculo de la
corrección
adecuada, la
pendiente que
buscamos es:
(-2.232+/-0.003) - (-0.8513+/-0.0007) = (-1.381+/-0.003)
donde para calcular el error hemos empleado la expresión
(4).
De la formula (1) podemos deducir:
![]()
![]()
Calculemos ahora el campo magnético B al que sometimos la
muestra, con su
error, usando las
expresiones (2) y
(3) para IB
= 1.99 A.
B = 228+/-11 mT
Por lo
tanto, RH
será (usamos
formula (4) para
calcular el error
y d = 0.1Cm. (figura
3)):
|
RH = -6.0E-3+/-0.3E-3
mT-1 |
|