¿Qué es Magnitud de escala Richter? |
Los sismólogos usan la escala de magnitud para representar la energía sísmica liberada por cada terremoto. A continuación se presenta una tabla con los efectos típicos de los terremotos en diversos rangos de magnitud:
Magnitud en escala Richter Efectos del terremoto
Menos de 3.5 Generalmente no se siente, pero es registrado
3.5-5.4 A menudo se siente, pero sólo causa daños menores.
5.5-6.0 Ocasiona daños ligeros a edificios.
6.1-6.9 Puede ocasionar daños severos en áreas donde vive
mucha gente.
7.0-7.9 Terremoto mayor. Causa graves daños.
8 o mayor Gran terremoto. Destrucción total a
comunidades cercanas
Aunque cada terremoto tiene una magnitud
única, su efecto variará grandemente según la distancia, la condición del
terreno, los estándares de construcción y otros factores. Los sismólogos usan
diferentes valores de la escala de Intensidad Mercalli para describir los
distintos efectos de un terremoto.
Cada terremoto tiene una cantidad única de energía, pero los valores de
magnitud dados por los diferentes observatorios sismológicos para un mismo
evento pueden variar. Dependiendo del tamaño, la naturaleza y la ubicación de
un terremoto, los sismólogos ultilizan diferentes métodos para estimar la
magnitud. En el caso de muchos eventos, es difícil estimar la magnitud con una
precisión de más de 0.2 unidades, y los sismológos frecuentemente verifican
las magnitudes estimadas a través de la obtención y análisis de datos
adicionales.
Para los sismólogos resulta más útil catalogar cada terremoto según su energía intrínseca. Esta clasificación debe ser un número único para cada evento, y este número no debe verse afectado por las consecuencias de los terremotos que varian mucho de un lugar a otro.
Para tener una idea del tipo de energias involucradas en los terremotos, vamos a imaginar dos situaciones. En la primera, tenemos una pieza de roca en una mesa de laboratorio. Podemos romper esta roca si aplicamos la fuerza suficiente con un martillo o un gato hidráulico. La roca probablemente se romperá en dos pedazos, a lo largo de algún plano débil de la roca y podemos pensar acerca de este plano como en una "falla" muy pequeña.
Sabemos de acuerdo a la teoría física que la cantidad de energía necesaria para romper o fracturar un pedazo de roca, es igual a la fuerza requerida para romper esa roca, por la distancia de separación entre los pedazos triturados de la roca original
(Trabajo) = Fuerza x (Distancia)
(Energía) = (Presión) x (Area) x (Distancia)
(Momento) = (Rigidez) x (Area de la falla) x (Distancia deslizada)
Mo = u x A x d
(dyne-cm) = (dyne/cm2) x cm2 x cm
En la fórmula anterior, el "momento" de un terremoto es fundamental para comprender qué tan peligrosa puede ser una falla de determinado tamaño.
Ahora, para nuestro primer ejemplo de un pedazo de roca en una mesa del laboratorio, la rigidez, o la resistencia de cizallamiento de la roca es una presión en una periferia de unos cientos de billones de dynes por centímetro cuadrado (la notación científica hace posible representar lo anteriormente expuesto de una manera sencilla). La presión actuá sobre un área produciendo una fuerza, y se puede ver como la unidad "cm" cuadrado se cancela. Ahora si suponemos que la distancia que existe entre las dos partes antes de ser separadas, es aproximadamente de un centímetro, entonces podemos calcular la energía en la unidad dyne-cm como se muestra a continuación:
M0 = (3x1011) (dyne/cm2)x10 (cm) x10 (cm) x1 (cm)
= (3 x 1011) x 102 (dyne-cm)
= 3x1013 dyne-cm (erg)
De nuevo, resulta muy útil el uso de la notación científica, ya que un dyne-cm es una cantidad de energía pequeñísima.
Ahora vamos a considerar el segundo caso, el terremoto de Double Spring Flat en 12 de septiembre de 1994, el cual ocurrió cerca del kilómetro 25 al sureste de Gardnerville. Ya que estamos trabajando en centímetros, lo primero que tenemos que hacer, es explicar como convertir la falla de 15 kilómetros de longitud y 10 km de profundidad a centímetros. Sabemos que 100 mil centímetros es igual a un kilómetro; así podemos escribir la siguiente ecuación y dividir a ambos lados en "km" para obtener un factor igual a uno.
1 km = 105 cm, así 1 = 105 cm/(km)
Naturalmente, podemos multiplicar cualquier número por uno sin cambiar su valor, así lo hacemos para cancelar las unidades de kilómetro y representarlas adecuadamente en unidades de centímetro
M0 = 3x1011 (dyne/cm2)x10(km)x(105 cm/ km)x15(km)x(105 cm/km)x30(cm)
= 1.35x1025 dyne-cm (erg)
En este resultado el uso de la notación científica es aún más necesario. Podemos observar que este terremoto, el más grande en Nevada en 28 años, tiene 4.5x1011 veces mas energía que la que se aplicó para romper la roca en la mesa de laboratorio.
Vamos a observar la energía de nuestros dos casos, de algunos terremotos y otros fenomenos en la siguiente tabla; para esto usaremos una unidad de energía mayor: la cantidad de energía producida del explosivo "TNT"
Magnitud Equivalencia de la Ejemplos
Richter energía TNT (aproximado)
-1.5 1 gramo romper una roca en una mesa de laboratorio
1.0 6 onzas una pequeña explosión en un sitio de
construcción
1.5 2 libras
2.0 13 libras
2.5 63 libras
3.0 397 libras
3.5 1,000 libras Explosión de mina
4.0 6 toneladas
4.5 32 toneladas Tornado promedio
5.0 199 toneladas
5.5 500 toneladas Terremoto de Little Skull Mtn., NV, 1992
6.0 1,270 toneladas Terremoto de Double Spring Flat, NV, 1994
6.5 31,550 toneladas Terremoto de Northridge, CA, 1994
7.0 199,000 toneladas Terremoto de Hyogo-Ken Nanbu, Japon, 1995
7.5 1,000,000 toneladas Terremoto de Landers, CA, 1992
8.0 6,270,000 toneladas Terremoto de San Francisco, CA, 1906
8.5 31,550,000 toneladas Terremoto de Anchorage, AK, 1964
9.0 199,999,000 toneladas Terremoto de Chile, 1960
10.0 6.3 billion toneladas Falla de tipo San-Andreas
12.0 1 trillion toneladas Fracturar la tierra en la mitad por el
centro !! o energía solar recibida
diariamente en la tierra
Un "trillión" de tonelada de dinamita es una cantidad tremenda de energía. Sin embargo, tomemos en cuenta que la tierra recibe esta cantidad de energía solar diariamente.
El problema en la tabla anterior es el enorme rango de energias, de gramos a onzas, a libras, a toneladas, hasta megatons de TNT. Sería mucho más sencillo comunicar al público cual es la energía de los terremotos a través de una escala sencilla como la que se muestra en la tabla superior en la columna izquierda, con un rango que va de uno a diez.
Para transformar este rango astronómico de energías en una escala sencilla, podemos usar una herramienta matemática llamada logaritmo. Si nosotros elevamos el número diez a algun exponente "x", para obtener un número mayor "N"; entonces el "logaritmo" (log) de ese número mayor "N" es el valor del exponente "x":
10x = N asi log10N = x
Ahora vamos revisar el "log" (base 10) en algunos ejemplos:
------------------------------------------------------------------ N 1x1025 100 25 10 1 0.01 -1 ------------------------------------------------------------------ x=logN 25 2 1.4 1 0 -2 indefinido ------------------------------------------------------------------
Toma en cuenta que es posible sacarle el "log" a un número muy pequeño, pero no es posible sacar el "log" de ningun número negativo.
En los años 30, el Dr. Charles F. Richter desarrolló una escala de magnitud para terremotos a fin de representar adecuadamente las diferencias entre los terremotos pequeños y medianos que él observó en el sur de California, y los terremotos grandes que registró alrededor del mundo. El decidió cuál sería la pequeña cantidad de energía a la que se le asignaría la magnitud cero, y escribió una ecuación semejante a la que tenemos abajo. Se ultiliza el logaritmo para representar rangos de enorme energía de manera adecuada:
Ahora vamos usar esta ecuación (utilizada para energías representadas en unidades de dyne-cm) para estimar la magnitud de un diminuto terremoto que puede llevarse a cabo en una mesa de laboratorio:
M0 = 3x1013dyne-cm
Mw = (2/3)(log103x1013(dyne-cm)) - 16.0)
= (2/3)(13.5 - 16.0)
= (2/3)(-2.5)
= -1.7
Las magnitudes negativas son permitidas en la escala de Richter, aunque tales terremotos son muy pequeños.
A continiuación tomemos la energía hallada anteriormente para el terremoto de Double Spring Flat, y calculemos su magnitud:
M0 = 1.425
Mw = (2/3)(log101.4x1025(dyne-cm)) - 16.0)
= (2/3)(~ 25.2 - 16.0)
= (2/3)(9.2) = 6.1
La magnitud que obtenemos de 6.1 es casi igual a la magnitud reportada por el labolatorio sismológico de UNR, y por otros observatorios.
La mayoría de los sismólogos ultilizan métodos diferentes del que acabamos de usar para calcular la magnitud de los terremotos. El encontrar la longitud, profundidad y deslizamiento de una falla puede llevar varios días, semanas o incluso meses después de un gran terremoto. El mapeo de las fallas sísmicas que hacen los geólogos, o el dibujo de la distribución espacial de las réplicas como hacen los sismólogos, puede proporcionar estos parámetros después de un considerable esfuerzo. Pero algunos terremotos grandes y la mayoría de los pequeños, no presentan ni fallas superficiales ni tienen suficientes réplicas para poder estimar su magnitud en la forma que ultilizamos anteriormente. También, resulta de mucha ultilidad el poder calcular rápidamente la magnitud de un evento, así que cualquier medida de emergencia requerida puede llevarse a cabo cuando antes.
Una de las contribuciones más valiosas de Charles Richter fue el descubrir que las ondas sísmicas propagadas por todos los terremotos pueden proporcionar buenas estimaciones de sus magnitudes. El consiguió los registros de las ondas sísmicas de un gran número de terremotos, y desarrolló un sistema de calibración para medición de las magnitudes.
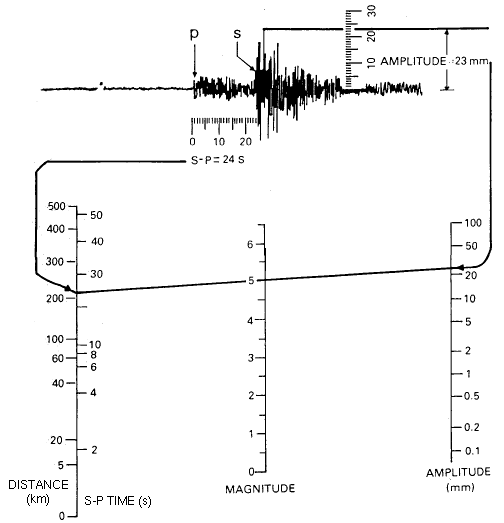
Richter demostró que entre mayor era la energía intrínseca de un terremoto, mayor era la "amplitud" de movimiento del terreno en una distancia dada. El Calibró su escala de magnitud usando la medida de "amplitud" máxima de la onda de cizallamiento (la onda S) en un periodo de 20 segundos, registrando los datos en un sismómetro altamente sensible a este tipo de ondas. Aunque inicialmente su trabajo fue calibrado únicamente por estos sismómetros específicos, y sólo para terremotos en el sur de California, los sismólogos han desarrollado factores de escala para ampliar la escala de magnitud Richter a muchos otros tipos de medición en todo tipo de sismómetros, y alrededor del mundo. De hecho, se han llevado a cabo estimaciones de magnitud para miles de terremotos en la luna y para dos temblores en el planeta "Marte".
El diagrama inferior muestra como usar el método original de Richter para calcular la magnitud por medio de un sismograma.

Por supuesto después de haber medido la "amplitud" de onda, usted tiene que calcular su logaritmo, y escalarlo por un factor según la distancia que haya entre el sismómetro y el terremoto, luego se calcula la magnitud a través de la diferencia de tiempo de S-P. Las escalas en el diagrama superior forman un nomograma que permite realizar el cálculo matemático rápidamente con sólo dar un vistazo. La ecuación que representa este nomograma es la siguiente:
M = log10A (mm) + 3log10(8(s)) - 2.92
Los sismólogos tratarán de obtener una estimación de magnitud separada de cada estación sísmica donde se registre el terremoto, para luego obtener promedio. Estos promedios reportados en los diferentes laboratorios sismólogicos justo en el momento posterior de un terremoto, comunmente difieren aproximadamente en un 0.2 unidades de magnitud. Cada laboratorio está calculando el promedio de las magnitudes obtenidas las diferentes estaciones a las tienen acceso. Pueden pasar varios dias para que las diferentes organizaciones que existen llegan a un consenso acerca de cuál fue la mejor estimación de magnitud.
Para estimar los efectos de un terremoto, los sismólogos emplean un método distinto de medición llamado intensidad. La intensidad no debe ser confundidad con la magnitud. Aunque cada terremoto tiene un sólo valor de magnitud, sus efectos varían de un lugar a otro, y por lo tanto habrá muchas estimaciones de intensidades diferentes. Usted puede leer acerca de la escala de Intensidad Mercalli, una forma común de clasificar los efectos de los terremotos.