1) Matriz A: conjunto de números reales
ordenados en filas y columnas,
A = 
; matriz
de m filas y n columnas.
2) Orden de una matriz A(m x n), m x n: indica el número de filas, m, y
de columnas, n, de una matriz.
3) Matriz cuadrada: matriz con igual número de filas que de columnas.
4) Matriz identidad de orden n, In: Matriz cuadrada de orden n
con unos en la diagonal y ceros fuera de ella.
4-1) Ejemplo: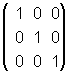 
matriz identidad de orden 3, I3.
5) Matriz inversa de una matriz A, A-1 (consultar también
producto de matrices):
matriz que verifica:× A-1× A = A× A-1 = I, con I
la matriz identidad.
A inversible (admite inversa) 
|A| 
0 (consultar
determinantes).
5-1) Ejemplo: si A =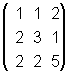 
,
A es inversible, pues |A| = 1 y
A-1 = 
, pues:
× 
= 
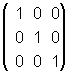y
× 
= 
.
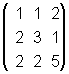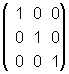6) Suma de matrices, A + B: matriz que resulta de sumar los elementos de A
y B que están situados en la misma fila y columna. Si A = (aij)
y B = (bij), matrices del mismo orden m x n,
A + B = (aij + bij), 
i
= 1 .. m, 
j
= 1 .. n.
6-1) Ejemplo: si A = 
y B = 
,
A + B = 
= 
.
7) Multiplicación de una matriz A por un escalar 
(número real): matriz que resulta de multiplicar todos los elementos de
la matriz A por el escalar 
.
7-1) Ejemplo: si A = 
y = 4,
4× 
= 
= .
8) Propiedades del producto de matrices.
8-1) El producto de matrices es asociativo: A× (B× C) = (A× B)× C.
8-2) El producto de matrices no es conmutativo, no
siempre se verifica:
A× B = B× A.
8-3) El producto de matrices es distributivo
respecto de la suma:
A× (B + C) = A× B + A× C.
9) Determinante de una matriz cuadrada A de orden 3,
|A| = :
(Regla de Sarrus) número que resulte de efectuar las operaciones:
a11× a22× a33 + a21× a32×
a13 + a31× a12× a23 -
- (a13× a22× a31 + a11× a32×
a23 + a33× a12× a21).
(diagonal principal y paralelas) (diagonal secundaria y paralelas)
9-1) Ejemplo: si A = 
,
|A| = 3× (-6) × 4 + 5× 7× (-1) + 2× 9× 8 - ((-1)× (-6)× 8 + 3× 7× 9 + 2× 5× 4) = -240.
10) El determinante de un producto de matrices es el producto de los
determinantes de las matrices.
10-1) Ejemplo:
=
= (-30)× (26) = -780.